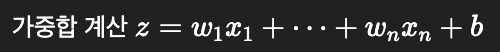🧠 딥러닝(Deep Learning)
1️⃣ 딥러닝이란 무엇인가?
💡 정의:
- 딥러닝(Deep Learning)은 인공신경망(ANN)을 여러 층으로 깊게 쌓은 구조를 의미하는 머신러닝 기술의 한 분야이다.
- "Deep"이라는 말은 3층 이상의 은닉층(Hidden Layer)을 갖는 구조를 의미한다.
- 입력층(Input Layer), 은닉층(Hidden Layer), 출력층(Output Layer)으로 구성된다.
- 인간의 뇌 구조인 생물학적 뉴런에서 영감을 받아 만들어졌다.
🧬 생물학적 뉴런 vs 인공뉴런:
| 생물 뉴런 | 인공 뉴런 |
| 덴드라이트: 입력 수신 | 입력값 x1,x2,...,xn |
| 세포체: 신호 처리 | |
| 축삭: 출력 전달 | 활성화 함수 적용 후 출력, |
2️⃣ 전통적 방법 vs 딥러닝 방법
# 전통적 방법 (Manual Feature Engineering)
- 입력: 이미지
- 중간: 사람이 정의한 특징 추출 (예: 눈과 눈 사이 거리, 코의 넓이, 입의 너비 등)
- 출력: 분류기 (SVM, Decision Tree 등)
- 단점: 사람이 일일이 특징을 정의해야 하므로 일반화가 어렵고 한계 존재
# 딥러닝 방법 (Automatic Feature Learning)
- 입력: 이미지
- 중간:
- 1층: 선과 경계 감지
- 2층: 눈/코/입 같은 중간 특징 감지
- 3층: 얼굴 전체 감지
- 출력: 자동 분류
- 장점: 특징을 자동으로 학습하므로 다양한 문제에 적용 가능
즉, 딥러닝은 하위 특징부터 고차 특징까지 점진적으로 추출하며 학습하는 구조를 가진다.
3️⃣ 딥러닝의 학습 흐름
① 순전파 (Forward Propagation)
- 입력값이 네트워크를 따라 전달되면서 가중치와 바이어스를 통해 연산됨.
- 각 레이어에서는:
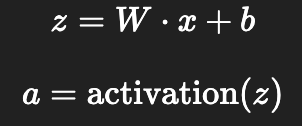
② 손실 계산 (Loss Calculation)
- 예측값과 실제 정답 사이의 차이를 수치로 계산함.
- 예시:


③ 역전파 (Backward Propagation)
- 손실 함수를 기준으로 각 가중치/바이어스가 손실에 얼마나 기여했는지 계산
- 연쇄법칙(Chain Rule)을 이용해 각 가중치의 gradient(기울기)를 구함
④ 가중치 업데이트 (Gradient Descent)
- 가중치와 바이어스를 다음과 같이 업데이트:
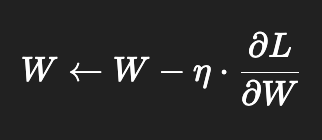
- η: 학습률(learning rate)
⑤ 반복 (Epoch)
- 전체 데이터를 여러 번 학습함 (epoch 수 만큼)
- epoch 1번 = 데이터셋 전체를 1회 학습
4️⃣ 딥러닝이 강력한 이유
- 표현력의 깊이
층이 많아질수록 더 복잡하고 추상적인 개념도 학습 가능 - 특징 자동 학습
사람이 일일이 정하지 않아도, 데이터에서 의미 있는 특징을 스스로 뽑아냄 - 엔드-투-엔드 학습 (End-to-End)
입력 → 출력까지 중간 과정을 전부 학습함
예: "이미지 → 숫자 분류", "음성 → 텍스트" - 범용성
이미지, 텍스트, 음성 등 거의 모든 데이터에 적용 가능
📌 그림 요약 (개념 흐름도)
입력 데이터
↓
입력층 (x1, x2, ..., xn)
↓
은닉층1: w₁·x₁ + w₂·x₂ + b₁ → f(z)
↓
은닉층2: ...
↓
출력층: 예측값 ŷ
↓
손실 계산 L(ŷ, y)
↓
역전파: ∂L/∂W, ∂L/∂b
↓
가중치 업데이트
↓
반복 (epoch)
⚙️ 요약 정리
| 항목 | 설명 |
| 딥러닝 | 인공신경망을 여러 층 쌓아 복잡한 패턴을 학습하는 기법 |
| 자동 특징 학습 | 전통적인 방식과 달리, 사람이 특징을 정의하지 않아도 됨 |
| 학습 흐름 | 순전파 → 손실계산 → 역전파 → 파라미터 업데이트 반복 |
| 핵심 수식 |
🧠 연쇄법칙 (Chain Rule)
1️⃣ 연쇄법칙이란?
합성함수의 미분을 계산하는 가장 중요한 수학 규칙
→ 복잡한 함수도 작은 함수로 쪼개서 각각 미분한 뒤 곱해서 전체 미분을 계산
📘 수학 정의:
함수 가 있을 때,
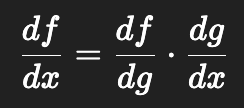
즉, 바깥 함수의 도함수 × 안쪽 함수의 도함수
2️⃣ 왜 연쇄법칙이 딥러닝에 중요한가?
딥러닝에서는 출력값이 단일 함수가 아니라, 수많은 함수들의 연쇄로 구성됨:
입력 x → z₁ = W₁·x + b₁ → a₁ = activation(z₁)
→ z₂ = W₂·a₁ + b₂ → a₂ = activation(z₂)
→ ... → L = 손실(a_n, y)
→ 전체는 거대한 합성함수 L=f(W,x)L = f(W, x)
→ 따라서 가중치 W가 손실 L에 얼마나 영향을 미치는지 계산하려면 반드시 연쇄법칙이 필요하다.
3️⃣ 신경망에 적용된 연쇄법칙
신경망에서:

이때, W1이 에 어떤 영향을 주는지 알고 싶으면?

→ 연쇄법칙을 단계적으로 적용한 역전파의 수식이라고 할 수 있다.
4️⃣ 연쇄법칙의 실제 의미
- 각 층의 gradient는 바로 다음 층의 gradient에 자신의 기여도만큼 곱해서 전달됨
- 그래서 딥러닝에서는 gradient가 연쇄적으로 곱해지며 흐름을 따라 역전파됨
📌 그림으로 보는 연쇄법칙 흐름
L(손실)
↑
∂L/∂a₂ (출력층의 기울기)
↑
∂a₂/∂z₂ (활성화 미분)
↑
∂z₂/∂a₁ (가중치 영향)
↑
∂a₁/∂z₁ (활성화 미분)
↑
∂z₁/∂W₁ (입력과 가중치)
⚙️ 요약 정리
| 항목 | 내용 |
| 연쇄법칙 | 합성함수의 미분 규칙. 바깥 × 안쪽 도함수 |
| 딥러닝에서의 역할 | 손실이 각 가중치에 얼마나 영향을 주는지 계산 |
| 왜 중요함? | 역전파에서 각 층의 gradient를 구하는 핵심 원리 |
| 핵심 수식 |
🧠 순전파(Forward Propagation) - 역전파(Backward Propagation)
1️⃣ 순전파란? (Forward Propagation)
📘 정의:
입력 데이터를 신경망에 통과시켜 출력값을 계산하는 과정 → 현재의 가중치와 바이어스로 예측값을 얻는 과정
🔁 흐름:
입력 x
↓
z₁ = W₁ · x + b₁ → a₁ = activation(z₁)
↓
z₂ = W₂ · a₁ + b₂ → a₂ = activation(z₂)
↓
...
↓
출력층 출력 aₙ = 예측값 ŷ
2️⃣ 손실 함수 계산
- 손실 함수(Loss function)는 모델이 정답과 얼마나 차이가 나는지 측정하는 함수이다.
- 예시:


3️⃣ 역전파란? (Backward Propagation)
📘 정의:
손실 함수의 오차를 기준으로, 가중치와 바이어스를 얼마나 조정해야 손실이 줄어드는지를 계산하는 과정
🔁 흐름 (역방향):
출력층에서 손실 계산 (L)
↓
∂L/∂aₙ (출력의 gradient)
↓
∂aₙ/∂zₙ (활성화 함수의 미분)
↓
∂zₙ/∂Wₙ, ∂zₙ/∂aₙ₋₁ (가중치, 이전층 출력에 대한 영향)
↓
∂L/∂Wₙ = 전체 gradient
↓
이전 층으로 전파 반복
→ 이게 바로 연쇄법칙을 활용한 역전파 흐름
4️⃣ 계산 예제
🧮 예: 뉴런 하나, 입력 2개, 편향 1개

5️⃣ 여러 뉴런의 계산 예 (은닉층 3개 뉴런)

→ 활성화 함수 적용 (예: ReLU) → 다음 레이어로 전달
6️⃣ 전체 흐름
| 단계 | 설명 |
| ① 순전파 | 입력값을 네트워크를 따라 계산해 예측값을 생성 |
| ② 손실 계산 | 예측값과 정답의 차이를 계산 |
| ③ 역전파 | 손실을 기준으로 각 가중치에 대한 gradient 계산 |
| ④ 가중치 업데이트 | gradient descent로 파라미터 조정 |
| ⑤ 반복 학습 | 이 모든 과정을 데이터셋 전체에 대해 여러 번 반복 (epoch) |
✅ 시각적 흐름 요약
입력 → 은닉층 → 출력 → 손실 계산
↓
역전파 시작
↓ ∂L/∂a → ∂a/∂z → ∂z/∂W
→ 각 W, b에 대한 기울기 계산
→ 옵티마이저가 업데이트
→ 다음 epoch로 반복
⚙️ 요약 정리
| 용어 | 설명 |
| 순전파 | 입력 데이터를 이용해 예측값 계산 |
| 역전파 | 예측값과 실제값의 차이를 바탕으로 가중치 조정 방향 계산 |
| 손실 함수 | 모델이 얼마나 틀렸는지 수치화 |
| 연쇄법칙 | 역전파에서 gradient를 전파하기 위해 사용되는 핵심 수학 원리 |
| 행렬 연산 | 실제 계산은 벡터/행렬 형태로 효율적으로 수행됨 |
🧠 XOR 문제 예측 신경망
1️⃣ XOR 문제란?
XOR (Exclusive OR)의 정의
- 두 개의 입력값이 다를 때만 1, 같으면 0을 출력하는 논리 연산
- 입력과 출력 테이블은 다음과 같다.
| x₁ | x₂ | y (XOR) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
❗ 중요 포인트:
- XOR 문제는 선형 분리가 불가능(non-linearly separable) → 즉, 단일 퍼셉트론(선형 모델)로는 해결할 수 없다.
2️⃣ 딥러닝의 필요 이유
단일 레이어(퍼셉트론 1개)로는 XOR 문제를 분리할 수 없다. 하지만 은닉층이 존재하는 다층 퍼셉트론(MLP) 구조라면,
비선형적인 경계를 학습할 수 있기 때문에 필요하다고 말할 수 있다.
3️⃣ XOR을 해결할 수 있는 MLP 구조
입력층 (2개 입력)
→ 은닉층 (뉴런 2~3개)
→ 활성화 함수 (ReLU 또는 Sigmoid)
→ 출력층 (1개 출력)
구조 요약:
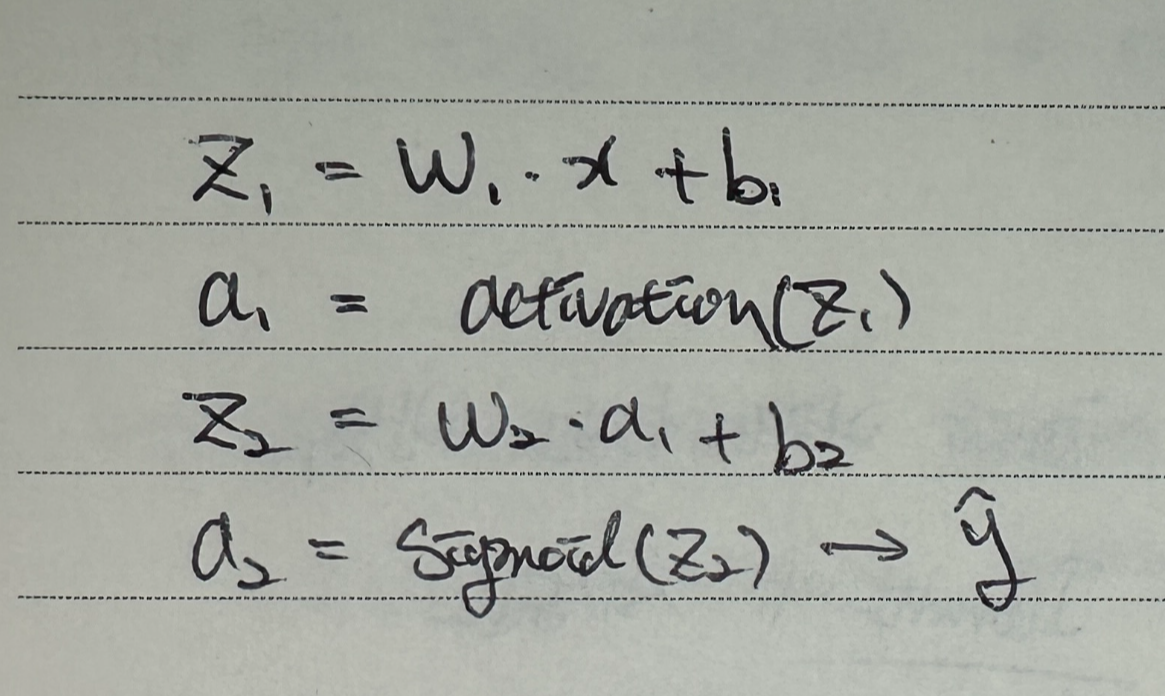
4️⃣ PyTorch 예제 코드 (기본 MLP 구조)
import torch
import torch.nn as nn
# XOR 입력 데이터: 4개의 샘플, 각 샘플은 2개의 입력 (0 or 1)
X = torch.tensor([[0,0],[0,1],[1,0],[1,1]], dtype=torch.float)
# XOR 정답값 (레이블): 입력 두 값이 다를 때만 1
y = torch.tensor([[0],[1],[1],[0]], dtype=torch.float)
# 신경망 모델 정의 - nn.Sequential은 층을 순차적으로 쌓을 수 있도록 도와줌
model = nn.Sequential(
nn.Linear(2, 3), # 입력 2개 → 은닉층 뉴런 3개로 연결 (가중치 W1, 바이어스 b1 포함)
nn.Sigmoid(), # 은닉층의 활성화 함수로 Sigmoid 사용 (비선형성 도입)
nn.Linear(3, 1), # 은닉층 3개 출력 → 최종 출력 뉴런 1개로 연결
nn.Sigmoid() # 출력층의 활성화 함수도 Sigmoid (결과를 0~1 사이 확률로 표현)
)
# 손실 함수 정의 - Binary Cross Entropy 사용 (이진 분류 문제이기 때문)
criterion = nn.BCELoss()
# 옵티마이저 정의 - SGD 사용, 학습률은 0.1
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
# 학습 루프 시작 (총 5000 epoch 학습)
for epoch in range(5000):
output = model(X) # 순전파: 입력 X에 대한 예측값 계산
loss = criterion(output, y) # 손실 계산: 예측값과 정답 y의 차이 측정
optimizer.zero_grad() # 역전파 전, 기존 gradient 초기화
loss.backward() # 역전파 수행: 각 파라미터에 대해 gradient 계산
optimizer.step() # 계산된 gradient를 이용해 파라미터 업데이트
# 일정 간격으로 손실값 출력
if epoch % 500 == 0:
print(f"Epoch {epoch}, Loss: {loss.item():.4f}")
1. 데이터 정의
X = torch.tensor([[0,0],[0,1],[1,0],[1,1]])
y = torch.tensor([[0],[1],[1],[0]])- XOR 연산을 학습하기 위한 입력-출력 쌍
- 2차원 입력, 1차원 이진 출력
2. 모델 구조
model = nn.Sequential(
nn.Linear(2, 3), # 2 → 3 연결 (입력층 → 은닉층)
nn.Sigmoid(),
nn.Linear(3, 1), # 3 → 1 연결 (은닉층 → 출력층)
nn.Sigmoid()
)- 총 2개의 Linear 계층 (완전 연결층)
- Sigmoid는 0~1 사이로 출력값을 제한 → 이진 분류에 적합
3. 손실 함수 & 옵티마이저
criterion = nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)- BCELoss: Binary Cross Entropy Loss, 확률 기반 분류 문제에서 주로 사용
- SGD: 경사하강법, 가장 기본적인 옵티마이저
4. 학습 루프
for epoch in range(5000):
...- 총 5000번 반복 학습
- loss.backward()가 역전파
- optimizer.step()가 파라미터 업데이트
학습 후 기대 결과:
Epoch 0, Loss: 0.73
Epoch 1000, Loss: 0.14
Epoch 5000, Loss: 0.01
결과적으로 학습이 잘 되면:
model(torch.tensor([[0,0]])) → 약 0
model(torch.tensor([[0,1]])) → 약 1
model(torch.tensor([[1,0]])) → 약 1
model(torch.tensor([[1,1]])) → 약 0
⚙️ 요약 정리
| 항목 | 설명 |
| XOR 문제 | 선형 분리 불가능. 전통 퍼셉트론으론 해결 불가 |
| 해결법 | 은닉층을 가진 MLP 구조 |
| 활성화 함수 | Sigmoid, ReLU 등으로 비선형성 도입 |
| 학습 흐름 | 순전파 → 손실 계산 → 역전파 → 반복 업데이트 |
| 학습 결과 | 4개의 입력쌍에 대해 올바른 분류 결과 도출 가능 |
이렇게 딥러닝에 대해 기초적인 부분을 정리해보았다. 딥러닝에 대해 배워본 적이 있어서 활성화 함수나 순전파, 역전파, 경사하강법 등에 대한 이해가 어렵지는 않았지만, 잘 기억이 나지 않는 부분도 있었고 처음 접해보는 개념들도 있었기에 차차 계속해서 학습하며 개념을 확립해가야할 것 같다.
계속해서 딥러닝 모델 등에 대한 개념과 코드를 정리하며 학습해나갈 예정이니 그때마다 갖는 의문이나 이해가 되지 않는 점들을 살펴보며 학습해야할 것 같다.
본 후기는 [카카오엔터프라이즈x스나이퍼팩토리] 카카오클라우드로 배우는 AIaaS 마스터 클래스 (B-log) 리뷰로 작성 되었습니다.